
皆さんは微分積分を理解していますか?多くの現代技術の基礎である微分積分は、すべての人に受け入れられているとは言い難いというのが現状です。
そんな微分積分ともっと仲良くなれそうな、東大生によって作られた二人対戦用のゲームがあります。それが『ナブラ演算子ゲーム』です。ナブラ演算子ゲームは、カード一式と、紙とペンがあれば遊ぶことができます。
ナブラ演算子とは、という記号で表される演算子のことです。
また、演算子とは、演算(計算)を表す記号の呼び方だと思ってください。
ナブラ演算子ゲーム
ナブラ演算子ゲームは、相手の「場」にある基底(場にある関数をこう呼ぶと思ってもらってえれば良いです)をいろいろな演算(微分したり、ゼロをかけたり、極限を取ったり)をすることによって消していき、相手の場にある基底をすべて消すことで勝ちとなるゲームです。
基底が消える条件は次の三つのうち少なくともどれか一つを満たしたときです。
- 演算により値が0になった。
- 演算により値が発散になった。
- 演算により、場の他の基底と線型従属になった。
ここでいう線型従属とは、ある基底が他の基底の定数倍でかけることを言います。例えば、![]() と
と ![]() は線型従属であると言えます。
は線型従属であると言えます。
たとえば、場にある ![]() を二階微分したり、
を二階微分したり、![]() に
に![]() を掛けると
を掛けると![]() になって消すことができますし、
になって消すことができますし、![]() を
を![]() について極限を取れば、発散して消すことができます。また、場に
について極限を取れば、発散して消すことができます。また、場に![]() が存在するときに
が存在するときに![]() を微分すれば、場は
を微分すれば、場は![]() となり、
となり、![]() と
と![]() は線型従属なのでどちらかが消えます。
は線型従属なのでどちらかが消えます。
ゲームの流れ
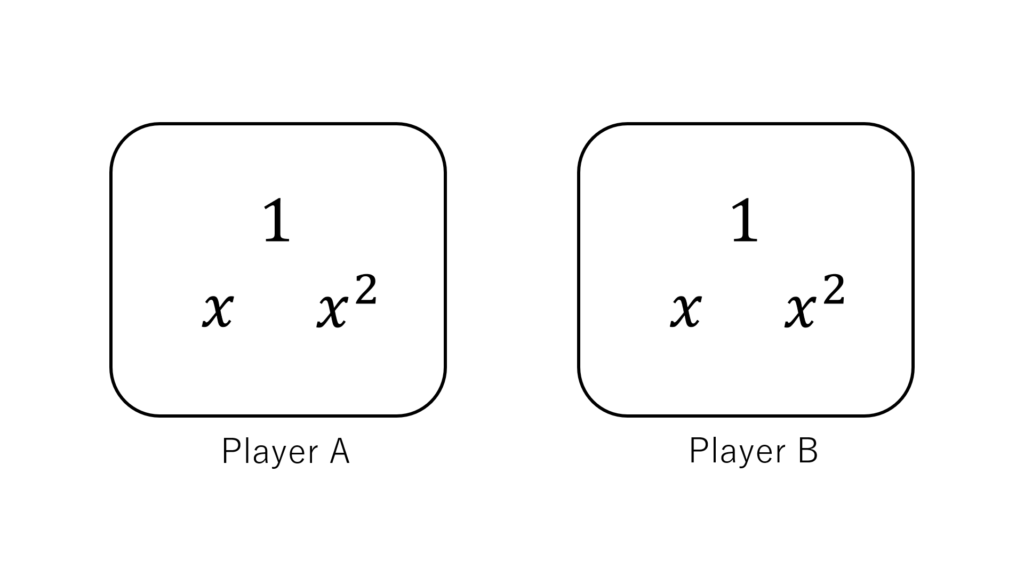
初めに、両プレイヤーは場に ![]() と、手札に7枚のカードを持ってゲームを開始します。
と、手札に7枚のカードを持ってゲームを開始します。
各プレイヤーが「操作」を互いに一回ずつ行い、自分の場の基底がすべて無くなる前に、相手のすべての基底を消去することを目的とします。
操作
操作とは、大まかに「基底を追加する」と「基底を演算する」の二つがあり、どちらか一つを行うことができます。
基底を追加する
手札にある関数カードの中から一枚を場に加えることができます。関数カードは次の7枚のみです。

基底を演算する
手札にある演算子カードを使って場の基底を演算することができます。演算子カードは次の14枚です。

演算子カード全てに共通するルールは
- 一回の操作で行える演算は一度だけ。
- 反則行為を行った場合には、その演算を行ったプレイヤーの負け。
- 演算のための計算はプレイヤーが行う。
- 計算できない場合、その演算を行ったプレイヤーの負け。
ですが、演算子ごとに微妙にルールが異なりますので、ルールや実例は別記事を参照してください。
 のルールと例(執筆中)
のルールと例(執筆中) のルールと例(執筆中)
のルールと例(執筆中) 系のルールと例(執筆中)
系のルールと例(執筆中)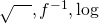 のルールと例(執筆中)
のルールと例(執筆中)
その他反則行為
ほかにも、以下のことをすると反則になります。
- 実数の範囲で定義できない演算
- 定義域に含まれない値にxを近づける演算
- 関数を振動させる極限を取る演算
何はともあれやってみよう
ナブラ演算子ゲームのカードは東京大学の学園祭である五月祭や、駒場祭で販売されていたり、東京大学本郷キャンパスの生協や東京大学生協通販サイトにて販売されているので、ぜひともゲットし、プレイしてみましょう!
・公式サイト:ナブラ演算子ゲーム
・購入:東京大学消費生活協同組合


